Funciones de segundo grado
Una función cuadrática es una función que puede ser descrita por una ecuación de la forma siguiente:
f(x) = ax2 + bx + c
Las letras a, b y c se llaman coeficientes de la función; la letra x representa la variable independiente
y la expresión f(x) representa el valor obtenido al reemplazar x por algún valor en el lado derecho de
la igualdad, es decir, f(x) es la imagen de x. La expresión f(x) puede reemplazarse por la letra y que
representa a la variable dependiente de la función.
La forma algebraica de una función cuadrática tiene las siguientes características:
• Siempre hay un término que contiene la variable elevada al cuadrado. La mayoría de las veces esta
variable se designa por la letra x, pero también se pueden usar otras.
• La expresión del lado derecho es un polinomio que tiene por lo general 3 términos, pero también puede
tener nada más que uno sólo; o solo 2. A veces una función cuadrática no está dada en su forma general, por lo
que es necesario aplicar algún procedimiento algebraico para transformarla, así en el ejemplo: f(x) = 2(x – 3)² + 3 queda: y = 2x² - 12x + 21.
Como ya se dijo, en una función cuadrática de forma f(x) = ax² + bx + c,las letras a, b y c se
denominan coeficientes; el coeficiente c de una función cuadrática se llama constante.
Representación gráfica de una función de segundo grado
En la gráfica aparecen representados los valores de y con respecto a x.
la posicion de esos puntos nos indica la forma de la curva; es una parábola, curba ilimitada.
El trazado de la curva uniendo entre si los puntos que hemos hallado de cada lado del eje y es aproximado. Cuantos más puntos se hallen, mayor aproximación se obtiene.
La operación de trazar la curva habiendo hallado solo algunos puntos de ella se llama interpolación, pues hacemos pasar la curva por muchos otros puntos que no hemos hallado, pero que suponemos pertenecen a la curva
En el gráfico de una parábola, además de su concavidad, se pueden apreciar los siguientes elementos
importantes:
• Eje de simetría
• Vértice
• Intercepto o valor de intersección en el eje Y
• Ceros o valores de intersección en el eje X
La curva es un círculo cuyo centro está en el origen. toda ecuación de la forma x2+y2=r2 representa un círculo cuyo radio es r
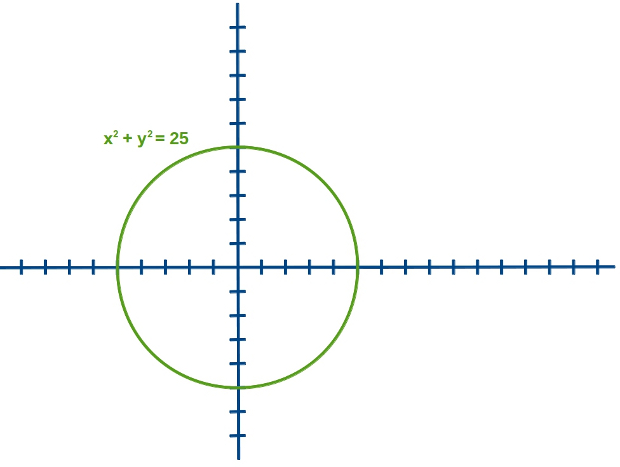
Toda ecuación de la forma a2x2+b2y2 = a2b2 o sea x2 + y2
b2 a2 representa una elipse
La curva se aproxima indefinidamente a los ejes sin llegar a tocarlos; los toca en el infinito. La curva obtenida es una hipérbola rectangular. Toda ecuación de la forma xy = a o y=a donde a es constante, representan una hipérbola de esta clase. x

La párabola, elipse y la hiperbola se llaman secciones cónicas o simplemente cónicas. El círculo es un caso especial de la elipse.
La función cuadrática y sus aplicaciones
Dado que la gráfica de una función cuadrática es una parábola de forma cóncava o
convexa, siempre será posible su valor mínimo o máximo. Esto es muy útil en
situaciones tales como maximizar utilidades o minimizar costos entre otras.
- Análisis de situaciones en diversos ámbitos que pueden ser modeladas a través de funciones cuadráticas.
- Maximizar o minimizar diversas situaciones tales como costos, ganancias, ventas, etc.
- Problemas físicos, como por ejemplo el lanzamiento de proyectiles
Para practicar más ejercicios sobre funciones cuadráticas puedes ingresar al link:
Elaboró: Xóchitl Herrera Luna

Comentarios
Publicar un comentario